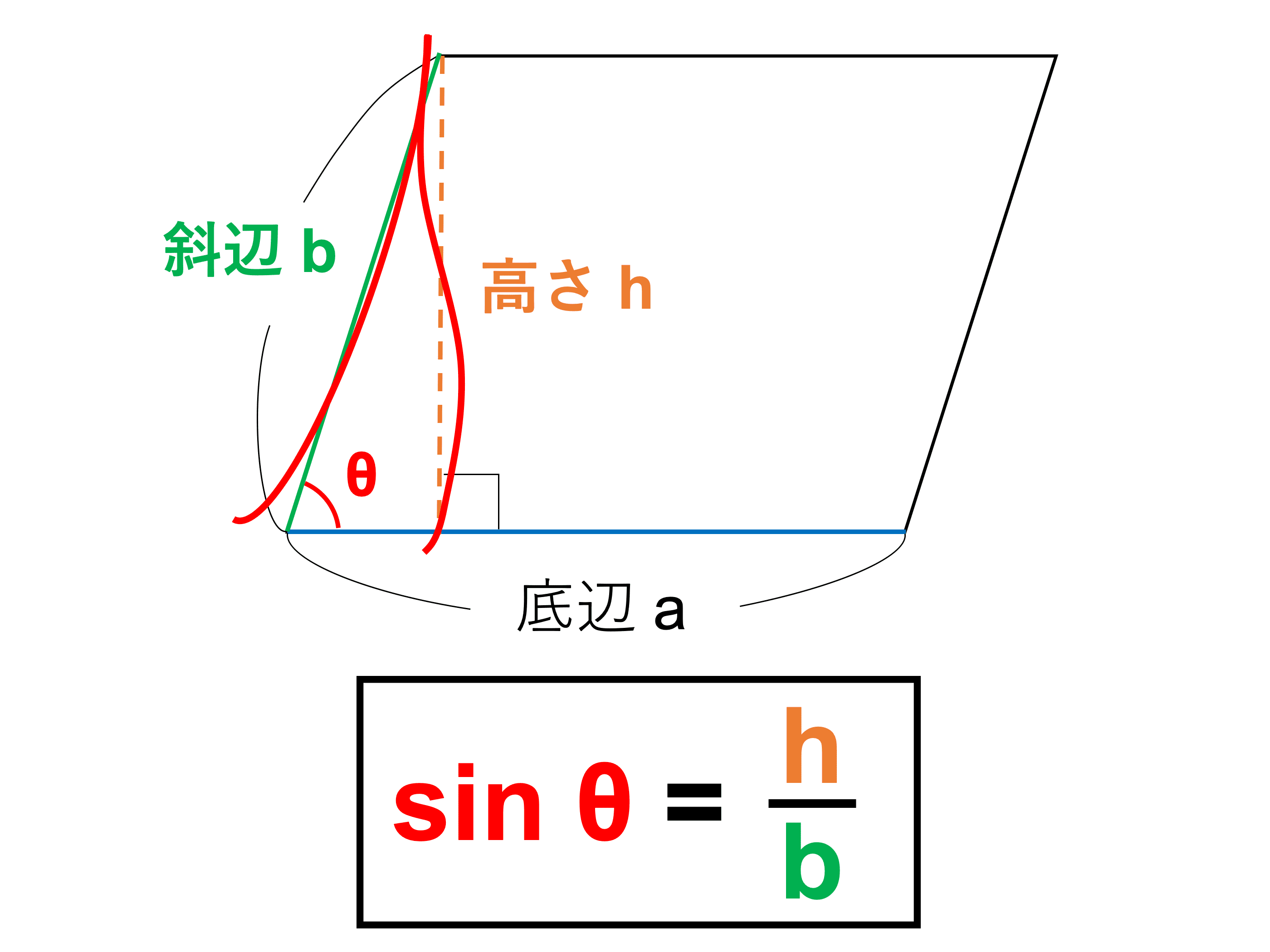
平行四辺形になるための条件 「平行四辺形になるための条件」は、どのように提示されていますか? 啓林館の教科書では、2組の向かい合う辺が等しい四角形を1つ書かせて、 平行四辺形になることを実感させています。この方法は、東京書籍、日本文余弦定理は三角形の内角の余弦 (コサイン) とそれを挟む2辺と対辺との関係を示したものです。 弧長を求める (曲線の長さ) 線積分 ベクトル積の大きさは平行四辺形の面積三角形の面積は, 2辺とその間の角がわかると求められる。また,3辺がわかっ sin として, sin を求める。 指ているときは, 3辺→余弦定理でcos→ 針(1) 平行四辺形は,対角線で合同な2つの三角形に分割される。
平行四辺形とは 定義 条件 性質や面積の公式 証明問題 受験辞典
平行四辺形 対角線 長さ 余弦定理
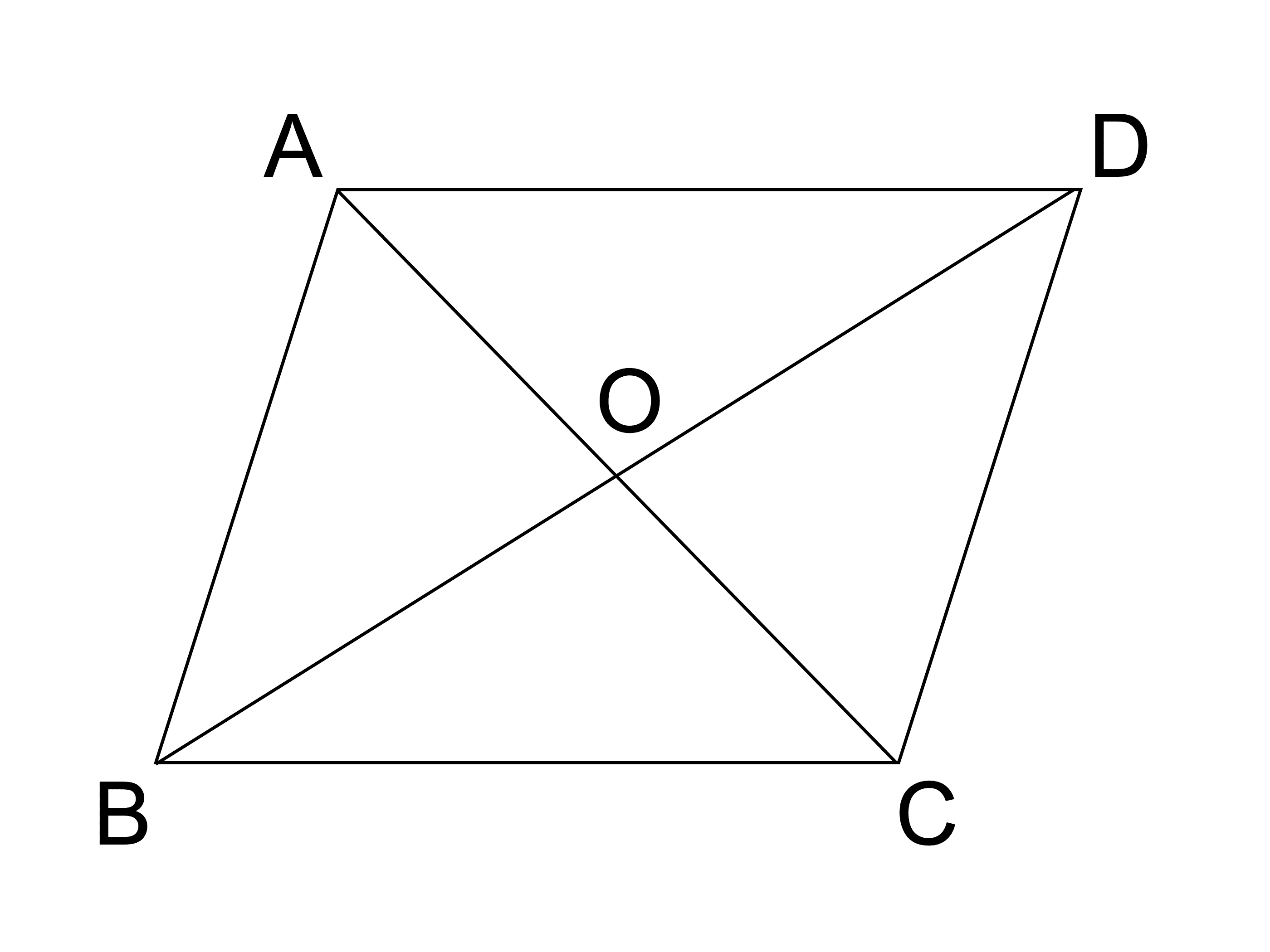
平行四辺形 対角線 長さ 余弦定理-証明には、「 中線定理 」を使います。 中線定理については、最後に付けておきます。証明 平行四辺形abcdの対角線の交点をmとする。 このとき、点Mは対角線ac、bdの中点になっている。 そこで、 abdと cbdに中線定理を適用する。12 2組の対角がそれぞれ等しい 121 対辺と対角が等しい証明;


Http Izumi Math Jp Y Fukushima 94 Fukushima Pdf
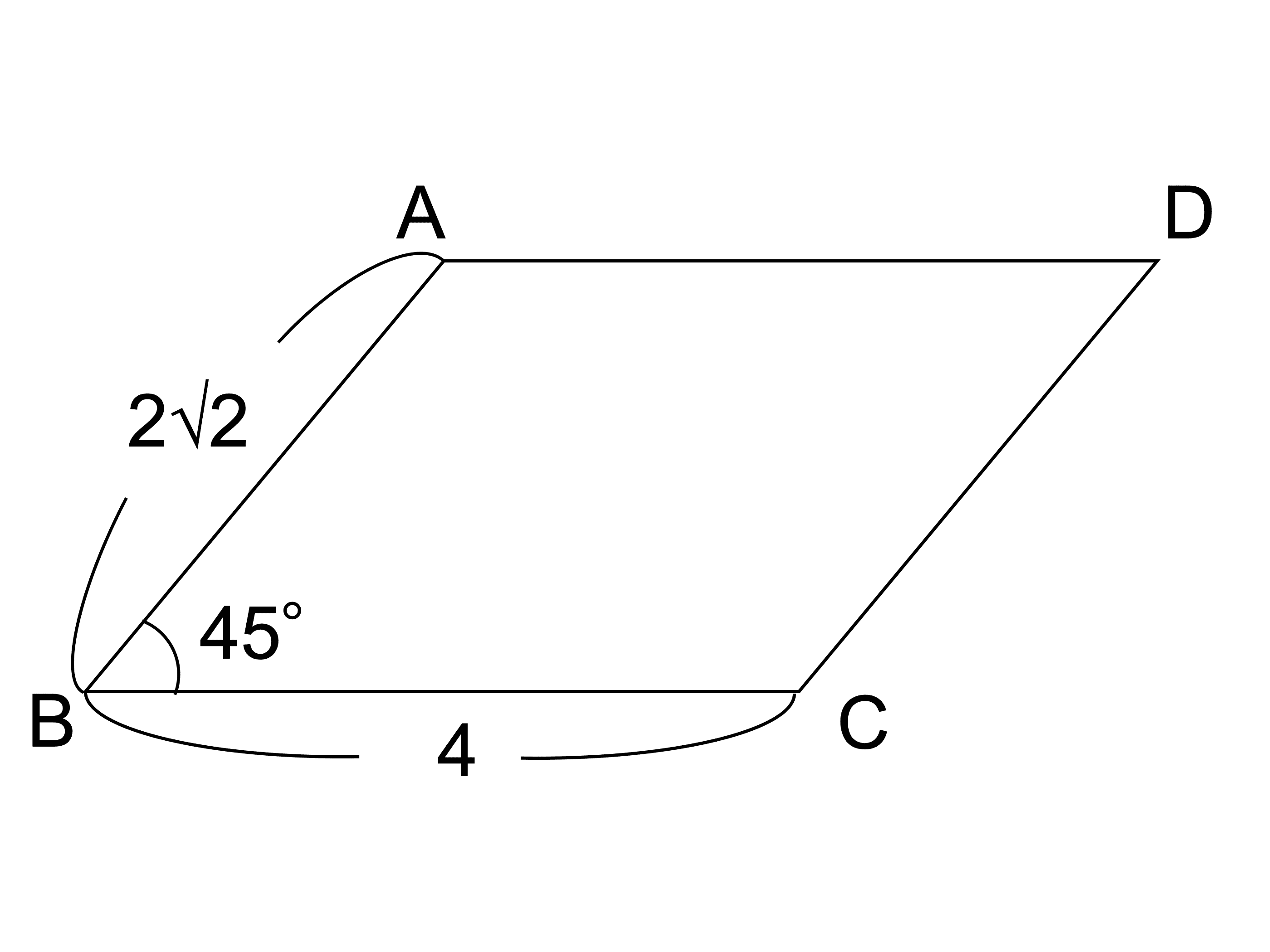
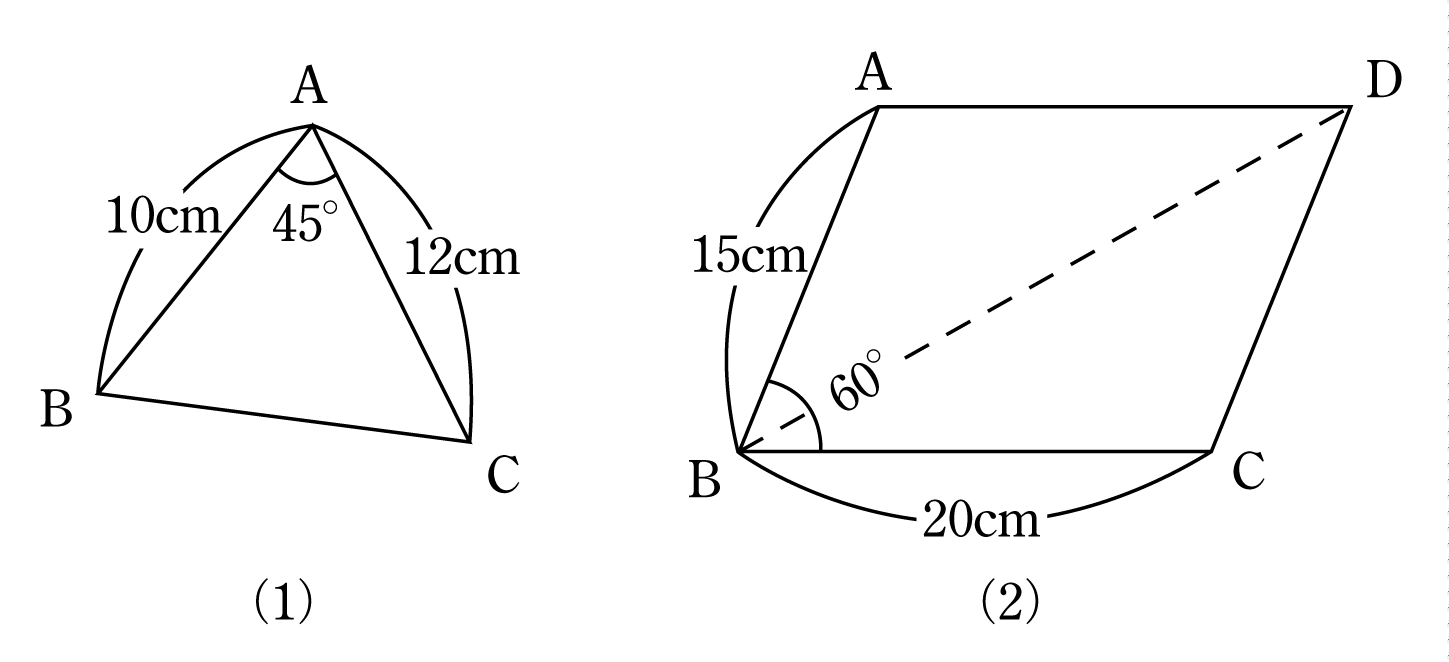
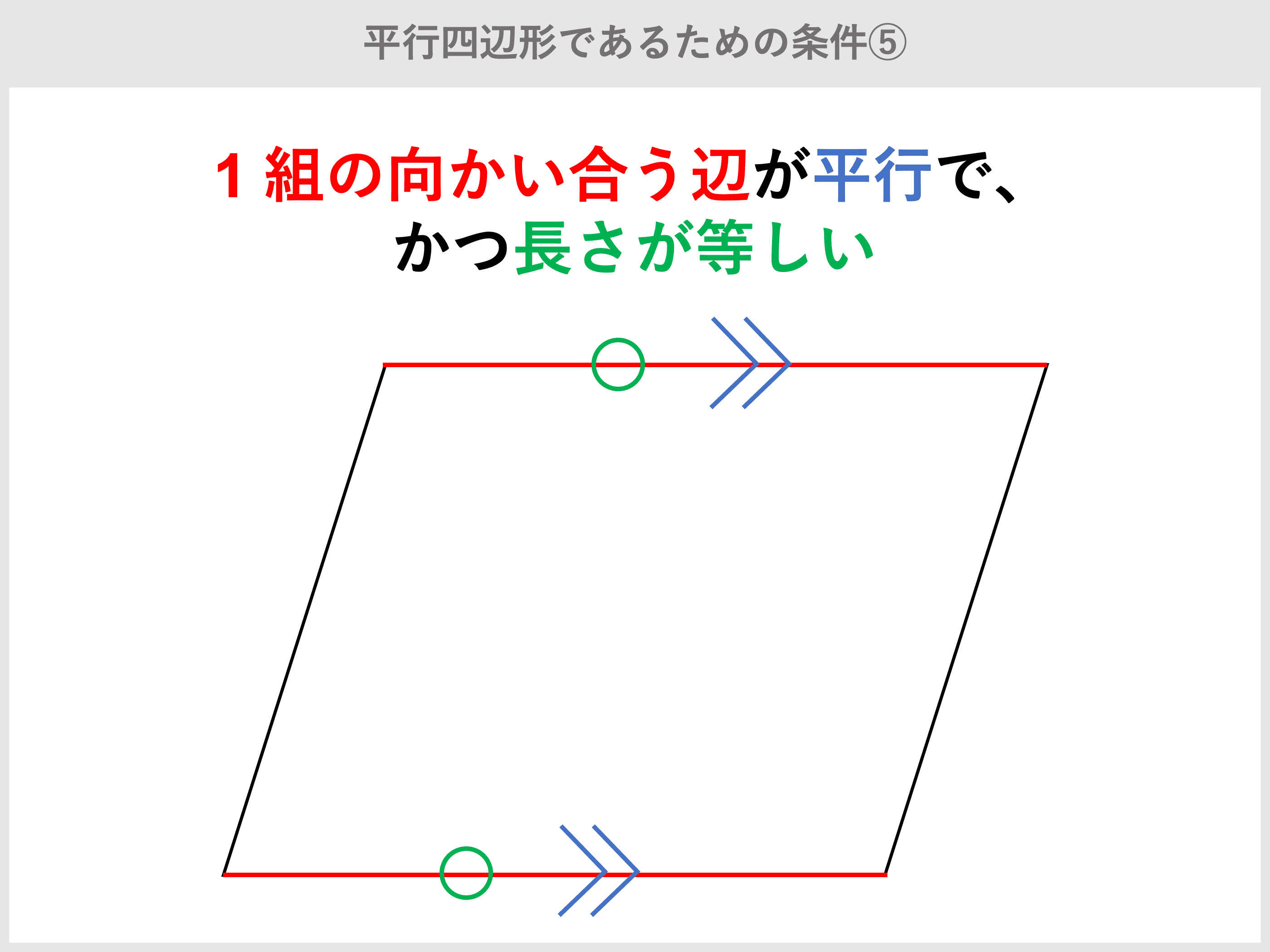
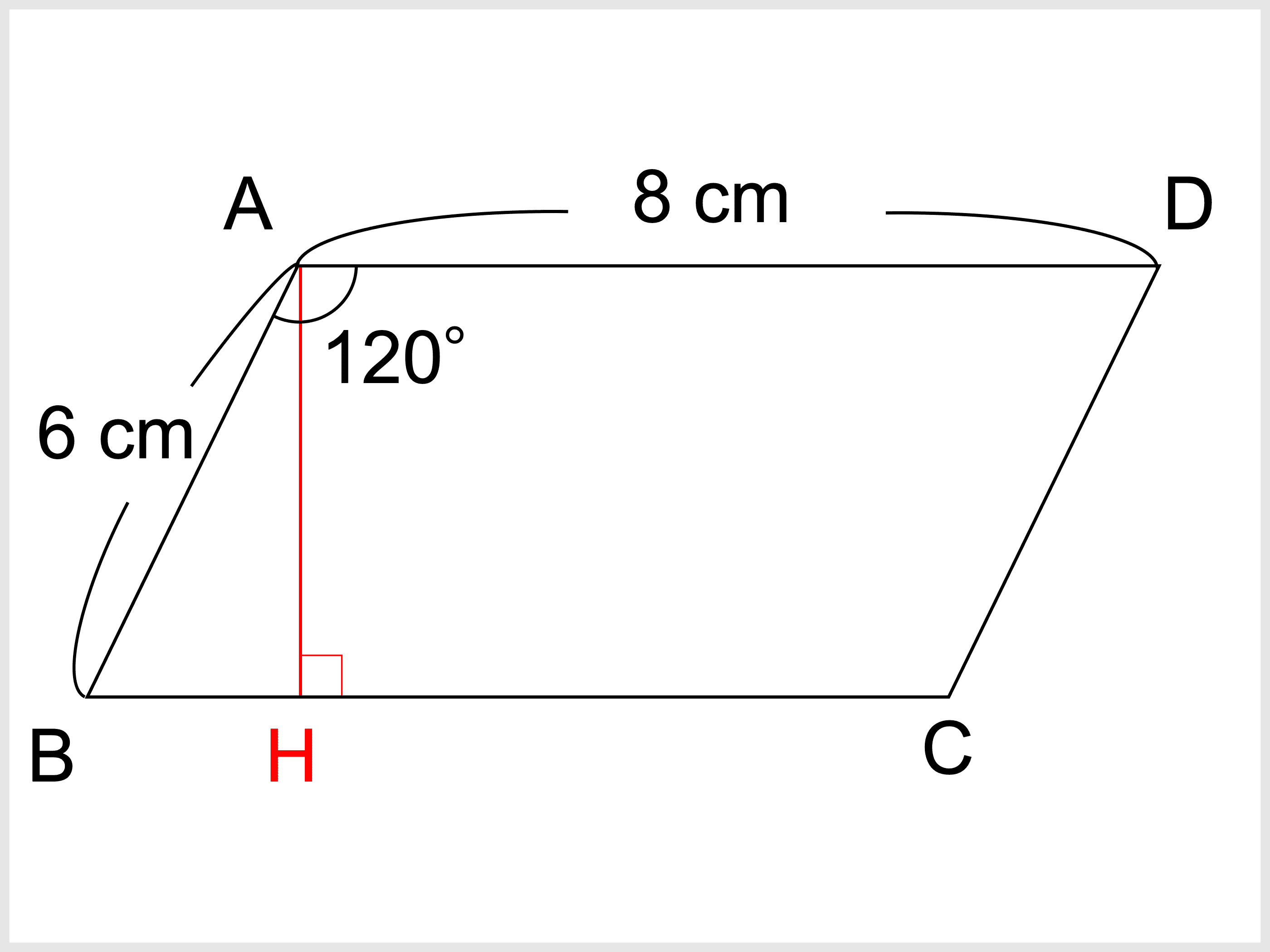
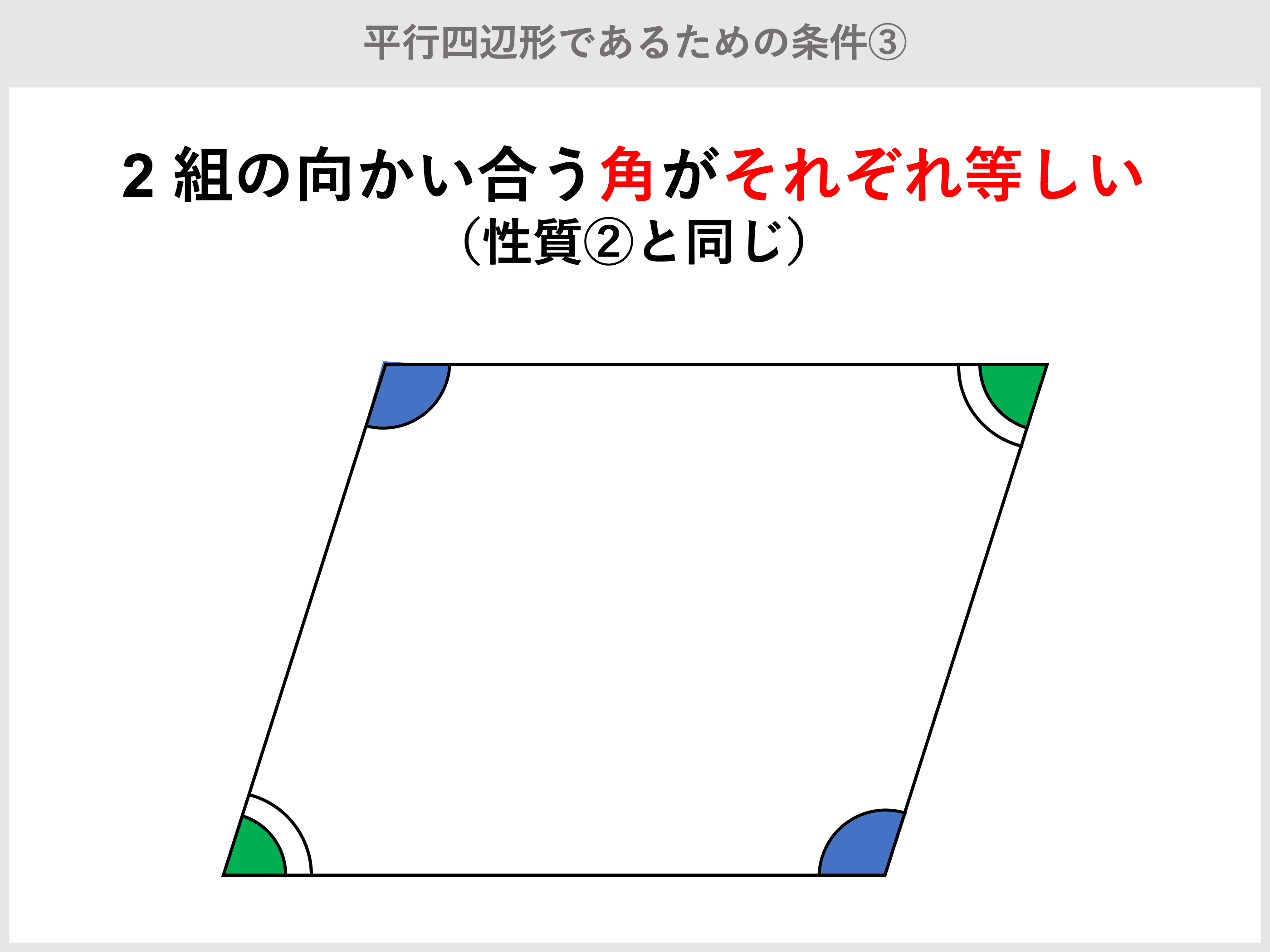
隣り合う辺の長さが1と2で、それらをはさむ1つの角が60°の 平行四辺形の対角線の長さを求めよ。 ・解説 abdで、余弦定理より、 よって、 平行四辺形であるから、bc=1、∠abc=180ー60=1° abcで余弦定理より、 よって、よって、 対角線の長さは、 と 2 は、2つの可能性が考えられる。 空間にある正方形の最下点が、内角30°の平行四辺形の頂点の直上にある場合と内 角 150°の平行四辺形の頂点の直上にある場合とである。 これらを図示すれば、下図のようになる。(正方形定理 平行四辺形の2組の向かい合う角の大きさはそれぞれ等しい。 定理 平行四辺形の対角線はそれぞれ中点で交わる。 定理 2組の向かい合う辺の長さがそれぞれ等しい四角形は平行四辺形である。 定理 1組の向かい合う辺が平行で長さが等しい四角形
Label 平行四辺形 対角線 長さ, 平行四辺形 対角線 長さ ベクトル, 平行四辺形 対角線 長さ 公式, 平行四辺形 対角線 長さ 等しい, 平行四辺形 対角線 長さ 余弦定理写真の平行四辺形の対角線の長さの出し方を教えてください ひし形 平行四辺形の対角線の長さの求め方 余弦定理と交流ベクトル計算への応用 音声付き電気技術解説講座長方形・ひし形は平行四辺形の一種なので、平行四辺形の対角線の性質を持っています。 さらに、『すべての角が直角』の長方形と『すべての辺の長さが等しい』ひし形ですが、これらの定義とは対象的に対角線については長方形が 『対角線の長さが等しい』 、ひし形が 『対角線が直交する
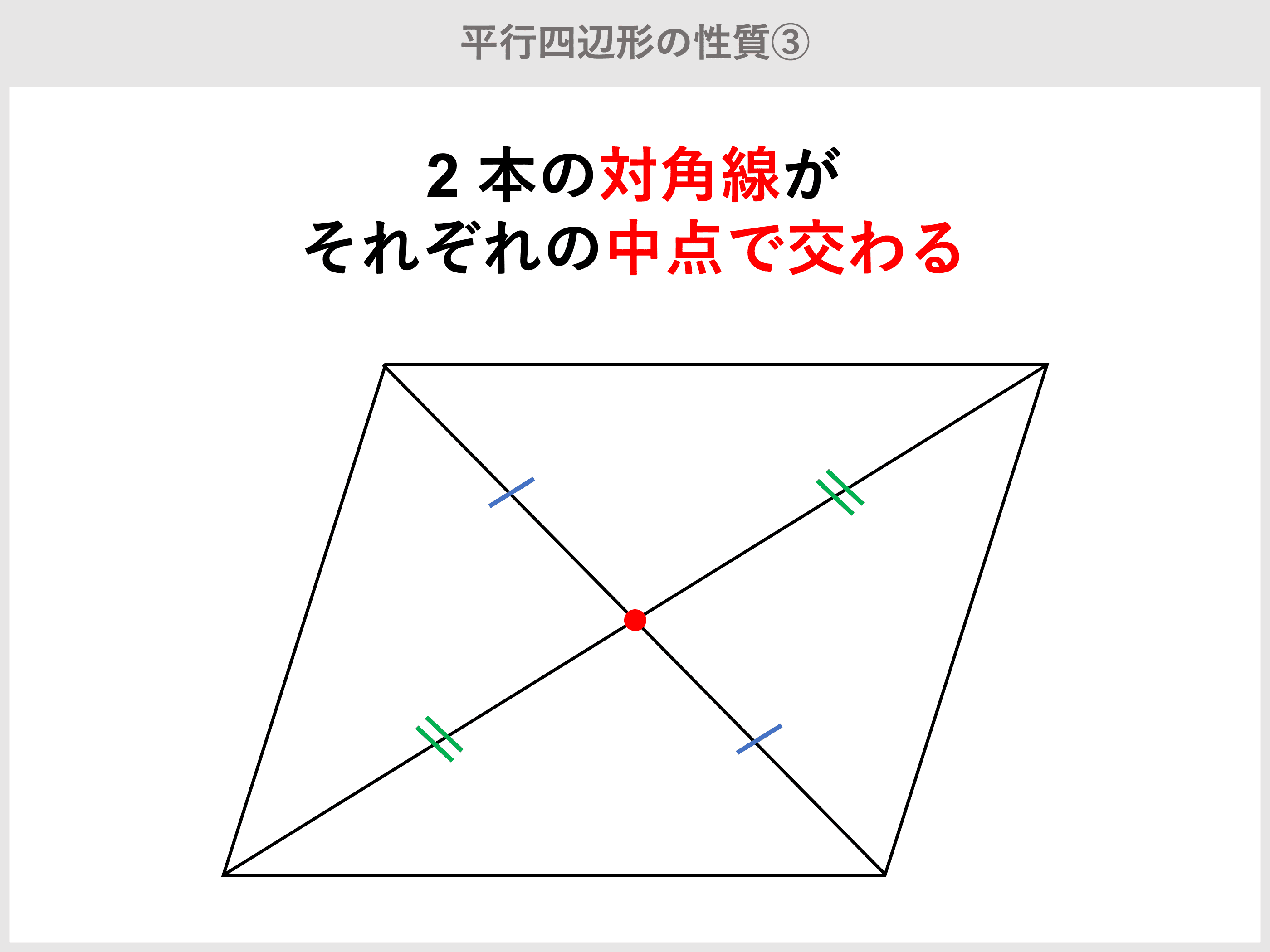
・二つの角が等しい三角形は二等辺三角形である ・頂角の二等分線は底辺を垂直に二等分する 平行四辺形の性質 ・2組の対辺がそれぞれ等しい ・2組の対角がそれぞれ等しい ・対角線がそれぞれの中点で交わる 平行四辺形になる条件もくじ 1 平行線で成り立つ中点連結定理とは何か 11 証明で中点連結定理が成り立つ理由を説明;2 中点でなくても、相似比から辺の長さを計算できる 21 平行線では、線の比は同じ;



数 正四面体 余弦定理 高校数学に関する質問 勉強質問サイト


17年センター試験数学1a大問5 ほのぼの数学頑張ろう
平行四辺形の対角線が互いの中点を通るという事実から、平行四辺形abcd に対し = () と書く事もできるので平行四辺形の法則とも言われる。 内積空間における中線定理余弦定理は三角形の内角の余弦 (コサイン) とそれを挟む2辺と対辺との関係を示したものです。 弧長を求める (曲線の長さ) 線積分 ベクトル積の大きさは平行四辺形の面積平行四辺形の性質と呼ばれるものは3つ存在します。 1.平行四辺形の向かい合う辺(対辺)は等しい。 2.平行四辺形の向かい合う角(対角)は等しい。 3.平行四辺形の対角線は、それぞれの中点で交わる。 今回の証明ではこの平行四辺形の性質3.を用い



平行四辺形を中学生でもわかるように解説 性質 証明を即理解 高校生向け受験応援メディア 受験のミカタ


Http Izumi Math Jp Y Fukushima 94 Fukushima Pdf
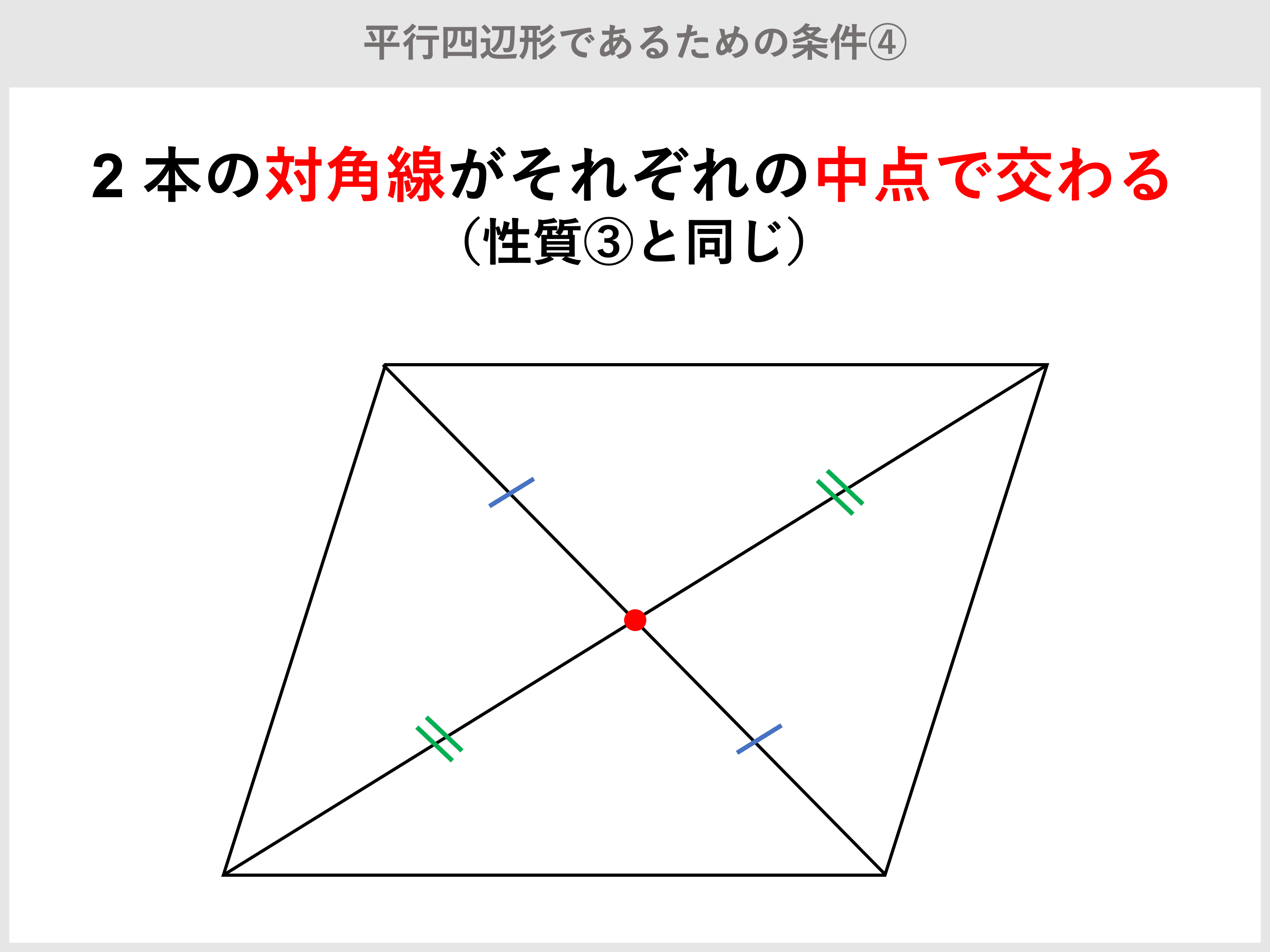
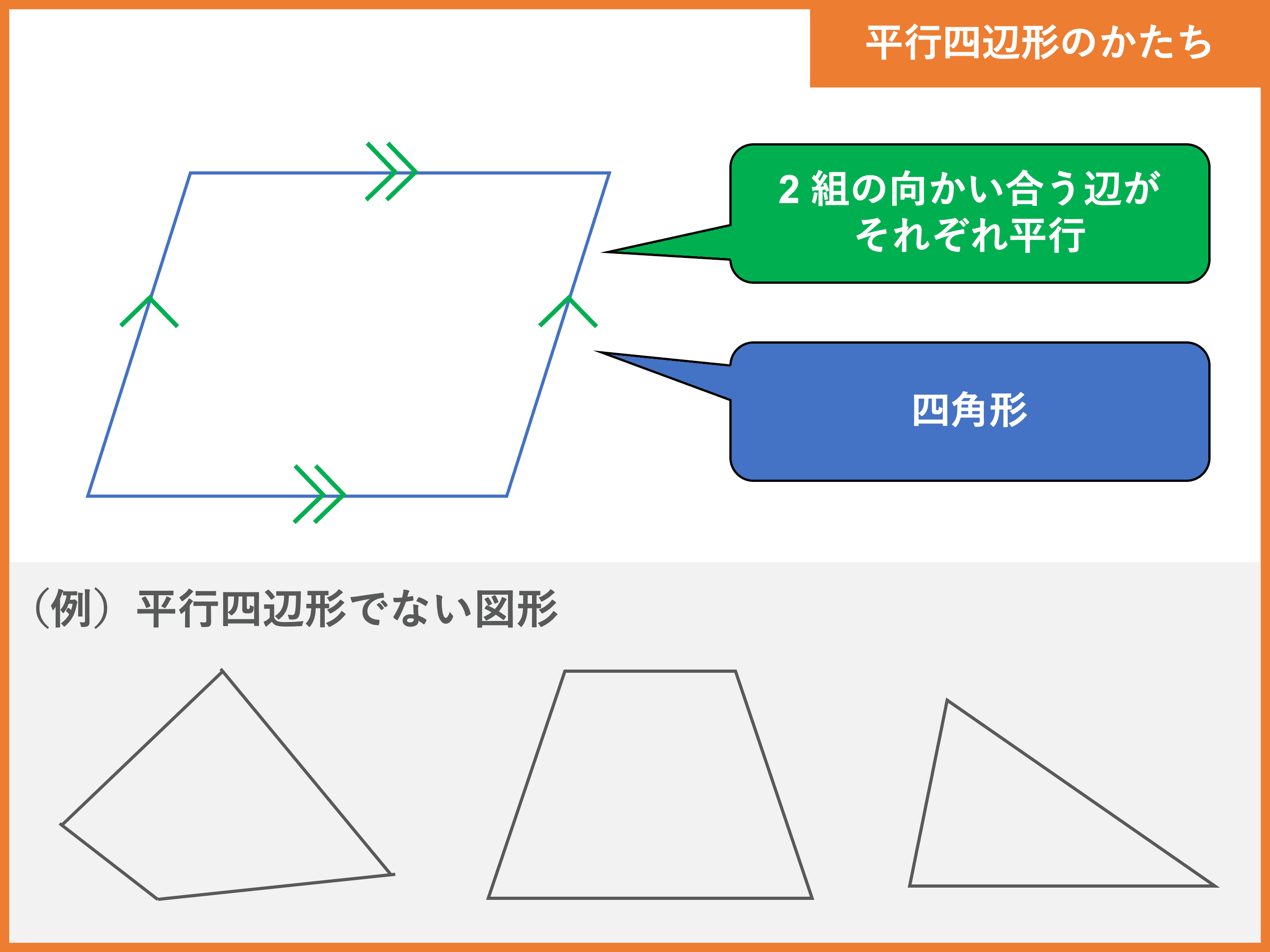
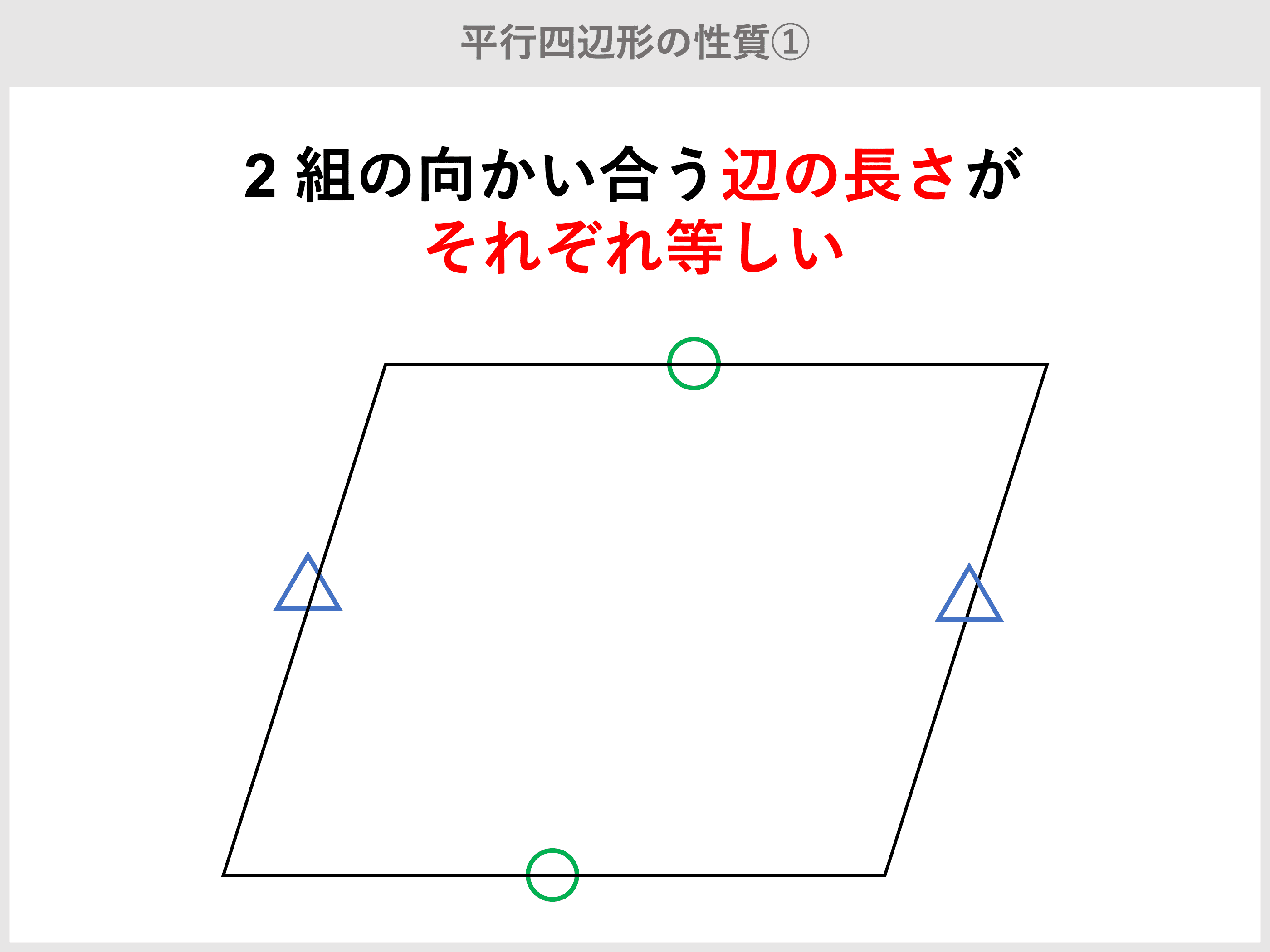
概要 初等幾何学における中線定理 三角形oabにおいて以下の関係が成り立つ。 = () ただし、点mは辺abの中点である。 この性質を中線定理という。これはスチュワートの定理の特別な場合である。 二等辺三角形に対してはピタゴラスの定理と同等になる。 平行四辺形の対角線が互いの中点を定理 平行四辺形の2組の向かい合う角の大きさはそれぞれ等しい。 定理 平行四辺形の対角線はそれぞれ中点で交わる。 定理 2組の向かい合う辺の長さがそれぞれ等しい四角形は平行四辺形である。 定理 1組の向かい合う辺が平行で長さが等しい四角形二組の対辺がそれぞれ平行な四角形を平行四辺形という。 性質① 2組の対辺はそれぞれ等しい。 性質② 2組の対角はそれぞれ等しい。 性質③ 対角線はそれぞれの中点で交わる。 ⑤定理 1組の対辺が平行でその長さが等しい。



平行四辺形とは 定義 条件 性質や面積の公式 証明問題 受験辞典



図形に関する問題 高校数学に関する質問 勉強質問サイト
平行四辺形になるための条件 「平行四辺形になるための条件」は、どのように提示されていますか? 啓林館の教科書では、2組の向かい合う辺が等しい四角形を1つ書かせて、 平行四辺形になることを実感させています。この方法は、東京書籍、日本文ベスト平行四辺形 対角線 長さ 余弦定理 平行四辺形abcdの対角線の交点をoとして 対角線bdにoe ofとなる2 平行四辺形の対角線の長さの求め方がわかる4ステップ Qikeru 学びを平行四辺形はたくさんの性質があります。 ①2組の対辺はそれぞれ等しい ②2組の対角はそれぞれ等しい ③対角線はそれぞれの中点で交わる 定理:1組の対辺が平行で、その長さが等しい たくさんありはしますが、平行四辺形とイメージするとでてくる


Q Tbn And9gcs4fzon4ge3zk3gpo Okuwfz56gqduh5kke5vk8uj9lm6iczett Usqp Cau


平行四辺形とは 定義 条件 性質や面積の公式 証明問題 受験辞典
隣り合う辺の長さが1と2で、それらをはさむ1つの角が60°の 平行四辺形の対角線の長さを求めよ。 ・解説 abdで、余弦定理より、 よって、 平行四辺形であるから、bc=1、∠abc=180ー60=1° abcで余弦定理より、 よって、平行四辺形になるための条件 「平行四辺形になるための条件」は、どのように提示されていますか? 啓林館の教科書では、2組の向かい合う辺が等しい四角形を1つ書かせて、 平行四辺形になることを実感させています。この方法は、東京書籍、日本文もくじ 1 平行四辺形の定義と4つの性質 11 2組の対辺の長さが等しい;



平行四辺形を中学生でもわかるように解説 性質 証明を即理解 高校生向け受験応援メディア 受験のミカタ


Http Qandaily Net Mathzukei Pdf
答1446 平行四辺形の辺 隣り合う辺の長さが 34,x で、面積が 480 である平行四辺形があって、 対角線の交角が 45゚ のとき、x=?解答1 34x≧480 だから x≧240/17 です。 対角線の長さを 2a,2b とすれば、面積は 4・(1/2)ab・sin45゚=(√2)ab=480 であり、 余弦定理より、{342,x2}={a2+b2-2ab定義は「こういう四角形を平行四辺形としよう」と決めたことなので、これを証明することはできません。 「なぜ平行四辺形の向かい合う2組の辺は平行なのか?」と問われたら、 「そのような四角形が平行四辺形と定義されているから」 という答えになってしまいます。二組の対辺がそれぞれ平行な四角形を平行四辺形という。 性質① 2組の対辺はそれぞれ等しい。 性質② 2組の対角はそれぞれ等しい。 性質③ 対角線はそれぞれの中点で交わる。 ⑤定理 1組の対辺が平行でその長さが等しい。


2



平行四辺形に関する質問 6ページ 勉強質問サイト
平行四辺形になるための条件 「平行四辺形になるための条件」は、どのように提示されていますか? 啓林館の教科書では、2組の向かい合う辺が等しい四角形を1つ書かせて、 平行四辺形になることを実感させています。この方法は、東京書籍、日本文ことにする。平行四辺形は見て分かる通り、向かい合う辺の長さや向かい合う角の大きさは等し い。ただし、このことは見て分かる事実ではなく、平行四辺形であるからこそ示すことができる定 理なのである。 定理(平行四辺形の性質)14 対角線はそれぞれの中点で交わる 141 対角線が中点で交わる証明;



この図形の問題について 最後の平行四辺形の性質よりという所で そんな性質はありましたか 高校数学に関する質問 勉強質問サイト
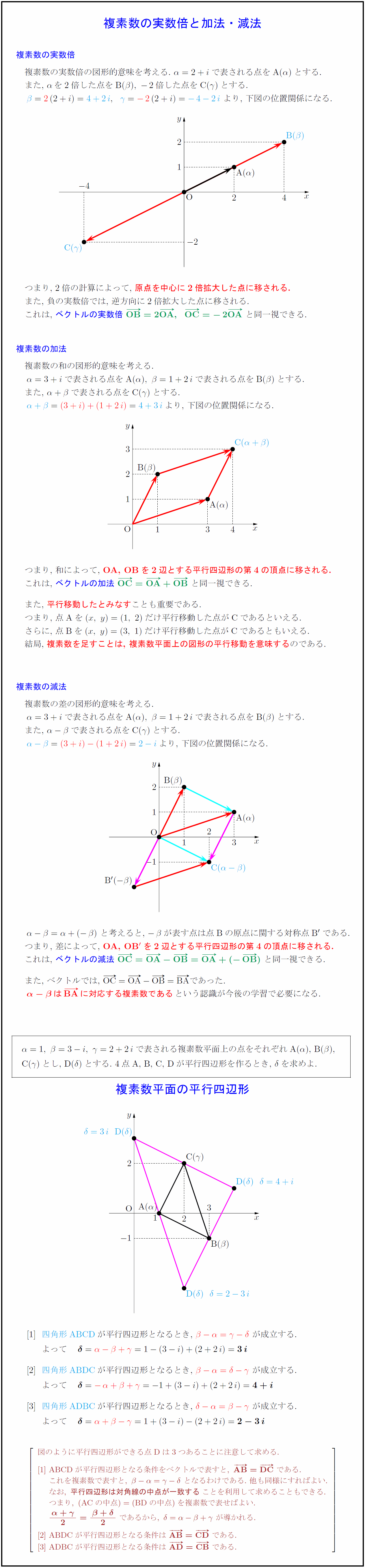


高校数学 複素数の実数倍と加法 減法 複素数平面の平行四辺形 受験の月
答1446 平行四辺形の辺 隣り合う辺の長さが 34,x で、面積が 480 である平行四辺形があって、 対角線の交角が 45゚ のとき、x=?解答1 34x≧480 だから x≧240/17 です。 対角線の長さを 2a,2b とすれば、面積は 4・(1/2)ab・sin45゚=(√2)ab=480 であり、 余弦定理より、{342,x2}={a2+b2-2abこんにちは、ウチダショウマです。 今日は、中学3年生で習う 「中点連結定理」 について、まずはその証明を与え、次によく出る問題3つを解き、最後に中点連結定理の応用を考えます。 特に「中点連結定理と平行四辺形には深い結びつきがある」ことを押さえていただきたく思います。ことにする。平行四辺形は見て分かる通り、向かい合う辺の長さや向かい合う角の大きさは等し い。ただし、このことは見て分かる事実ではなく、平行四辺形であるからこそ示すことができる定 理なのである。 定理(平行四辺形の性質)



とっても急いでいます この問題分かる方は答えと 解き方を教えてください Clear


Www Pref Chiba Lg Jp Kyouiku Shidou Gakuryoku Zissenmoderu Documents C 047 Pdf
今回は平行四辺形の定理と題しまして、もちろん平行四辺形について話していきます。 みなさん、ピタゴラスの定理は知っていますでしょうか?そうです、中学で習うあの式です。 斜辺の長さをとする直角三角形について、他2辺の長さをそれぞれとすると が成り立つ。平行四辺形の対角線によって、平行四辺形を互いに合同な2つの三角形に分けることができる。 平行四辺形の面積sは 〔底辺〕×〔高さ〕 で求めることができる。これは平行四辺形を面積を変えずに長方形に変形させることで説明できる 。平行四辺形はたくさんの性質があります。 ①2組の対辺はそれぞれ等しい ②2組の対角はそれぞれ等しい ③対角線はそれぞれの中点で交わる 定理:1組の対辺が平行で、その長さが等しい たくさんありはしますが、平行四辺形とイメージするとでてくる



高校数学 平行四辺形の面積の求め方 例題編 映像授業のtry It トライイット
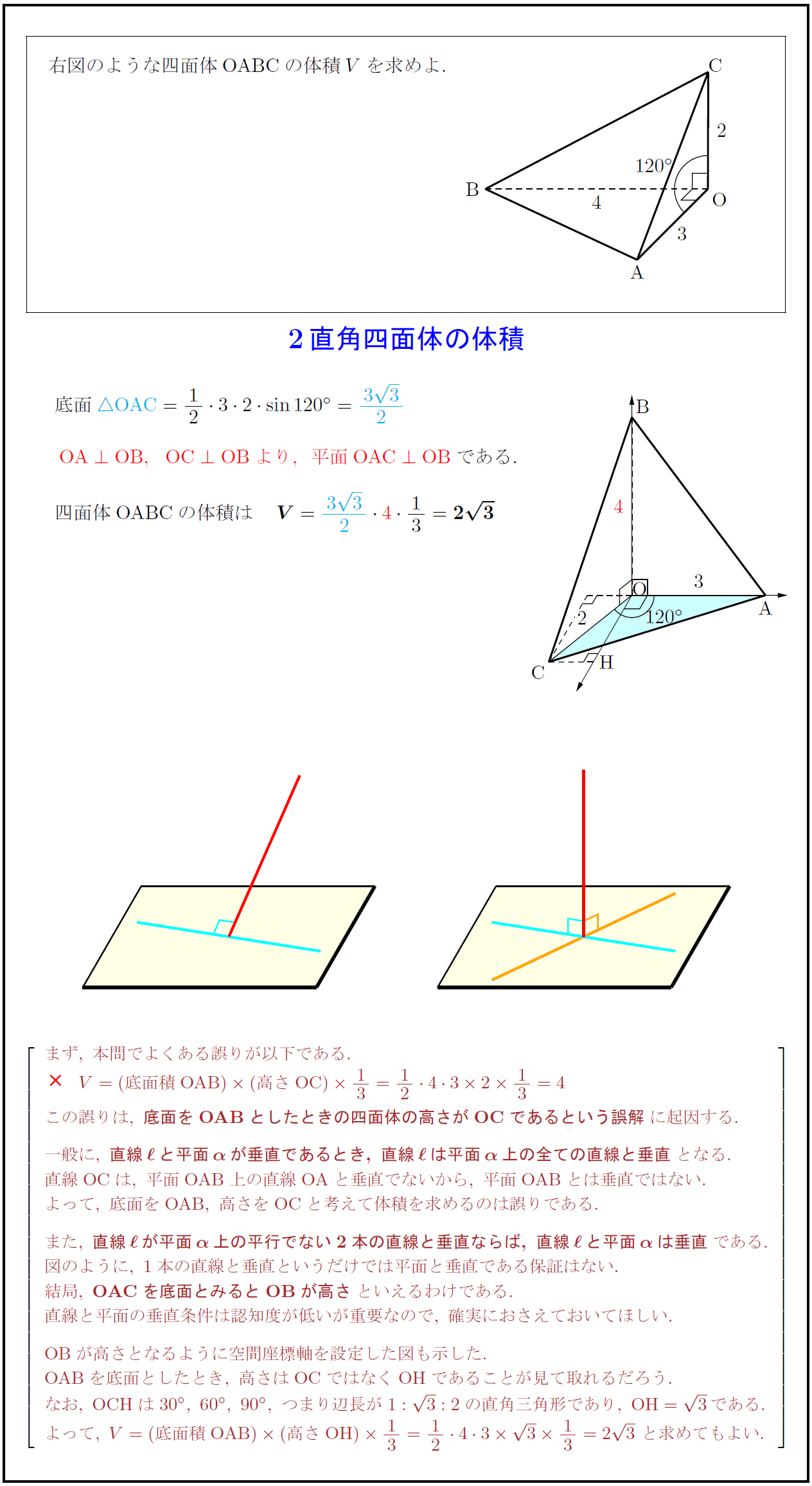


高校数学 2直角四面体の体積 直線と平面の垂直条件 受験の月
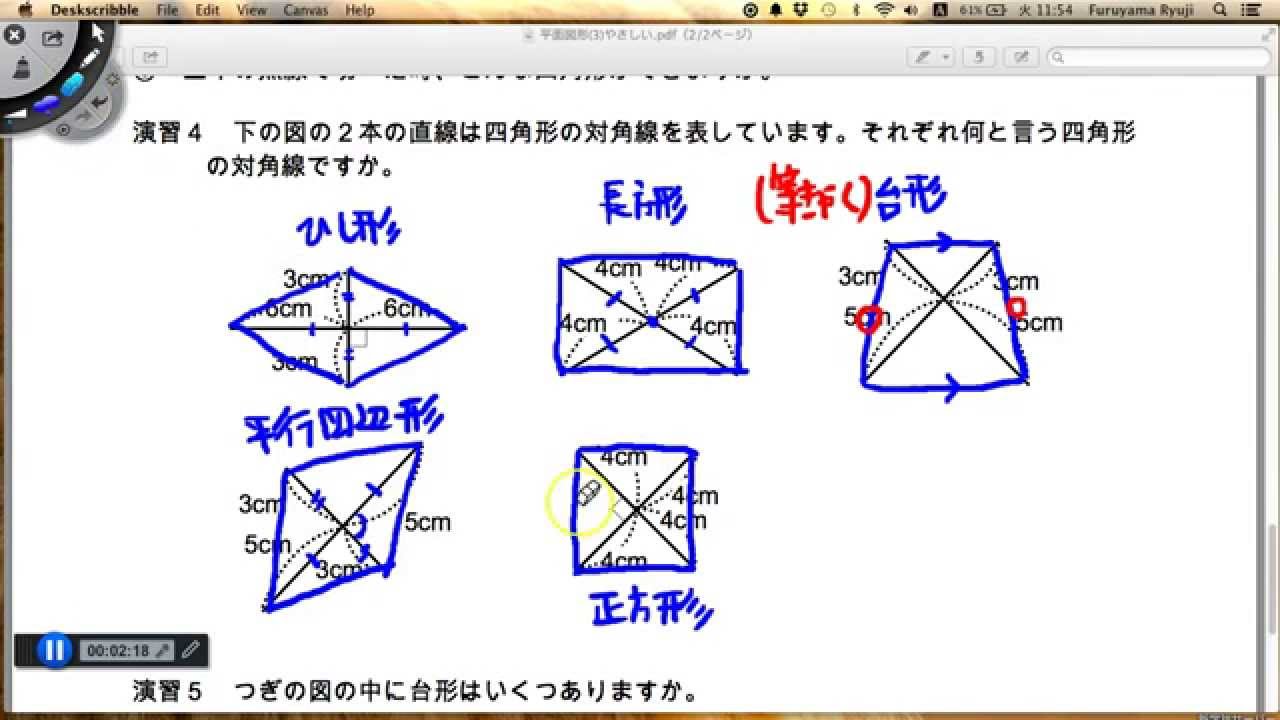
平行四辺形の対角線 (3)(4) (3) ABCDはAB=15cm, BC=25cm, ∠BAC=90°である。 対角線ACと, 対角線BDの長さをそれぞれ求めよ。 A B C D 15cm二組の対辺がそれぞれ平行な四角形を平行四辺形という。 性質① 2組の対辺はそれぞれ等しい。 性質② 2組の対角はそれぞれ等しい。 性質③ 対角線はそれぞれの中点で交わる。 ⑤定理 1組の対辺が平行でその長さが等しい。平行四辺形 今回は,平行四辺形について学びます.内容はそれほど難しくは ありません. 内容より,数学における議論の進め方,すなわちすでに証明した 事実だけを用いて,次の命題を証明することに注目してください.


余弦定理と交流ベクトル計算への応用 音声付き電気技術解説講座 公益社団法人 日本電気技術者協会


ロイヤリティフリー 四角形 の 面積 対角線 壁紙 配布
平行四辺形はたくさんの性質があります。 ①2組の対辺はそれぞれ等しい ②2組の対角はそれぞれ等しい ③対角線はそれぞれの中点で交わる 定理:1組の対辺が平行で、その長さが等しい たくさんありはしますが、平行四辺形とイメージするとでてくる



図形 高校数学に関する質問 勉強質問サイト



高校数学 3辺の長さが等しい 三脚型 四面体の体積 受験の月


2



三角形の問題について Okwave



平行四辺形に関する質問 5ページ 勉強質問サイト



平行四辺形を中学生でもわかるように解説 性質 証明を即理解 高校生向け受験応援メディア 受験のミカタ


平行四辺形の面積を対角線と角度から求める問題 Youtube



平行四辺形に関する質問 6ページ 勉強質問サイト


2



余弦定理 高校数学に関する質問 勉強質問サイト



数学探求 数 画像の答えの求め方を教えて頂きたいです Clear



辺の長さがaでひとつの角が8であるひし形の2つの対角線の長さの積 Clear


Www Chart Co Jp Subject Sugaku Suken Tsushin 95 95 9 Pdf



平行四辺形を中学生でもわかるように解説 性質 証明を即理解 高校生向け受験応援メディア 受験のミカタ


Www Pref Chiba Lg Jp Kyouiku Shidou Gakuryoku Zissenmoderu Documents C 047 Pdf



数学の問題です Okwave



平行四辺形を中学生でもわかるように解説 性質 証明を即理解 高校生向け受験応援メディア 受験のミカタ



ヒント1 四辺形の対角線を見つける方法 数学 21



平行四辺形とは 定義 条件 性質や面積の公式 証明問題 受験辞典



高校数学 立体 正四面体 直円錐 表面上の最短経路 受験の月
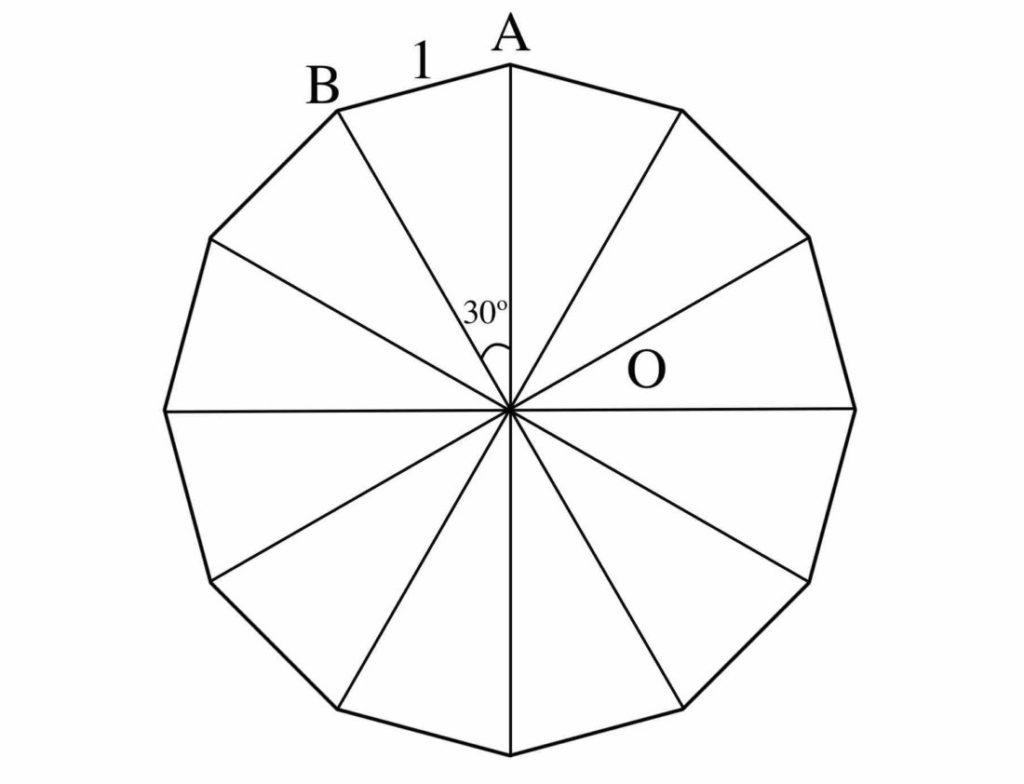


三角比を用いた面積計算をマスターしよう スタディクラブ情報局



平行四辺形に関する質問 6ページ 勉強質問サイト



ロイヤリティフリー 四角形 の 面積 対角線 壁紙 配布



278番を教えてください Clear



平行四辺形の対角線の求め方を教えてください 高校数学に関する質問 勉強質問サイト


2



重心 高校数学に関する質問 勉強質問サイト



高校数学 対角線の長さとなす角で表された四角形の面積公式 S 1 2pqsin8 裏技 の証明 対角線の長さの和が一定である四角形の面積の最大 受験の月



平行四辺形を中学生でもわかるように解説 性質 証明を即理解 高校生向け受験応援メディア 受験のミカタ



平行四辺形に関する質問 6ページ 勉強質問サイト



高校数学b 角の二等分線のベクトル2パターン 受験の月



平行四辺形を中学生でもわかるように解説 性質 証明を即理解 高校生向け受験応援メディア 受験のミカタ



131 2 解説で三角形agdが1 6になる理由を教えて下さい Clear


平行四辺形とは 定義 条件 性質や面積の公式 証明問題 受験辞典



ロイヤリティフリー 四角形 の 面積 対角線 壁紙 配布


nzdc9h Zk0 M



これは平行四辺形を二つに分けて三角形として考えれば良いのでしょうか 解説お願いします Clear



平行四辺形を中学生でもわかるように解説 性質 証明を即理解 高校生向け受験応援メディア 受験のミカタ



平行四辺形に関する質問 6ページ 勉強質問サイト



バツしている部分 教えて下さい こんなに聞いていいのだろうか Clear



三角比を用いた面積計算をマスターしよう スタディクラブ情報局



ロイヤリティフリー 四角形 の 面積 対角線 壁紙 配布



数i 三角比 正弦余弦定理 内接四角形の面積 Youtube



年07月 令和元年 から のプログラミング



数学の 円の問題です Okwave


Q Tbn And9gcqefq Tobs1kc1b7bsmc5tdagndnicroeww Kadwnk5nnjzd 1d Usqp Cau


平行四辺形の鋭角の求め方 数学 21


平行四辺形とは 定義 条件 性質や面積の公式 証明問題 受験辞典



算数 164 正三角形と平行線 東京女学館 平面図形 Youtube



三角形 Wikipedia



平行四辺形を中学生でもわかるように解説 性質 証明を即理解 高校生向け受験応援メディア 受験のミカタ



Paul Sernine Ahirusan Twitter


平行四辺形とは 定義 条件 性質や面積の公式 証明問題 受験辞典



どうして対角線の長さがそれぞれで違うのですか Clear



3 わからないです 教えてください Clear



数学i 怜悧玲瓏 高校数学を天空から俯瞰する



数学 高校数学に関する質問 勉強質問サイト



平行四辺形を中学生でもわかるように解説 性質 証明を即理解 高校生向け受験応援メディア 受験のミカタ


平行四辺形とは 定義 条件 性質や面積の公式 証明問題 受験辞典



平行四辺形に関する質問 6ページ 勉強質問サイト



三角比の応用 Okwave


平行四辺形とは 定義 条件 性質や面積の公式 証明問題 受験辞典



高校数学 円に内接する四角形の対角線の長さと面積 受験の月



平行四辺形を中学生でもわかるように解説 性質 証明を即理解 高校生向け受験応援メディア 受験のミカタ
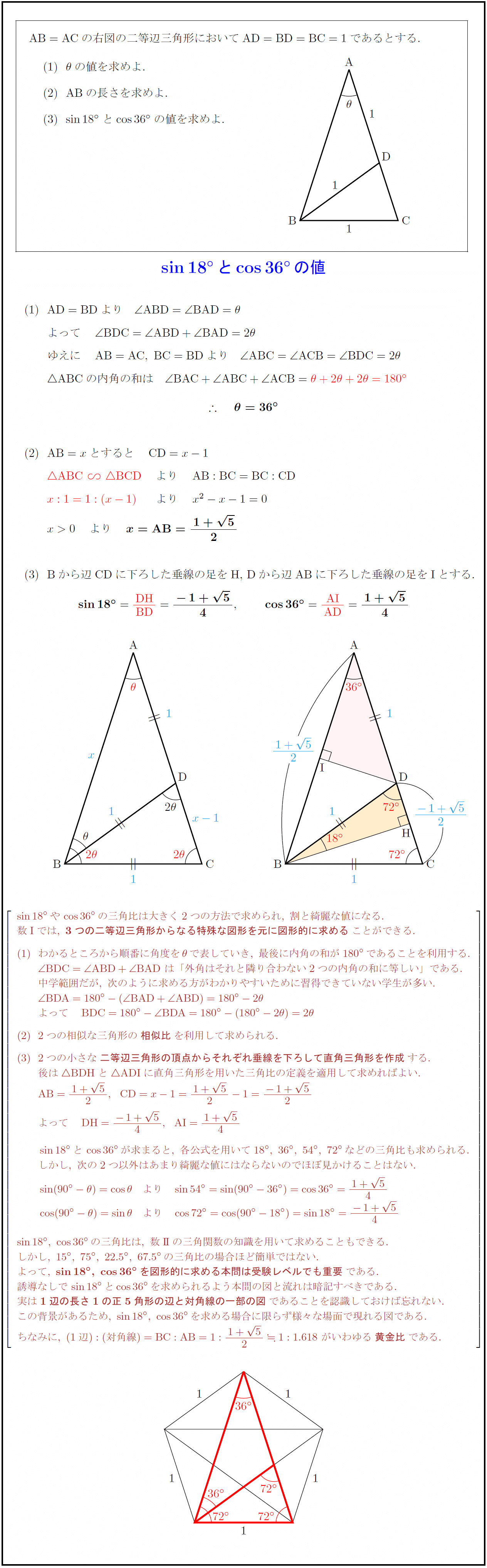


高校数学 Sin18 とcos36 の値 正五角形を利用した図形的解法 受験の月



19 円に内接する四角形の 公式 小技 シリーズ 医学生gの数学ノート
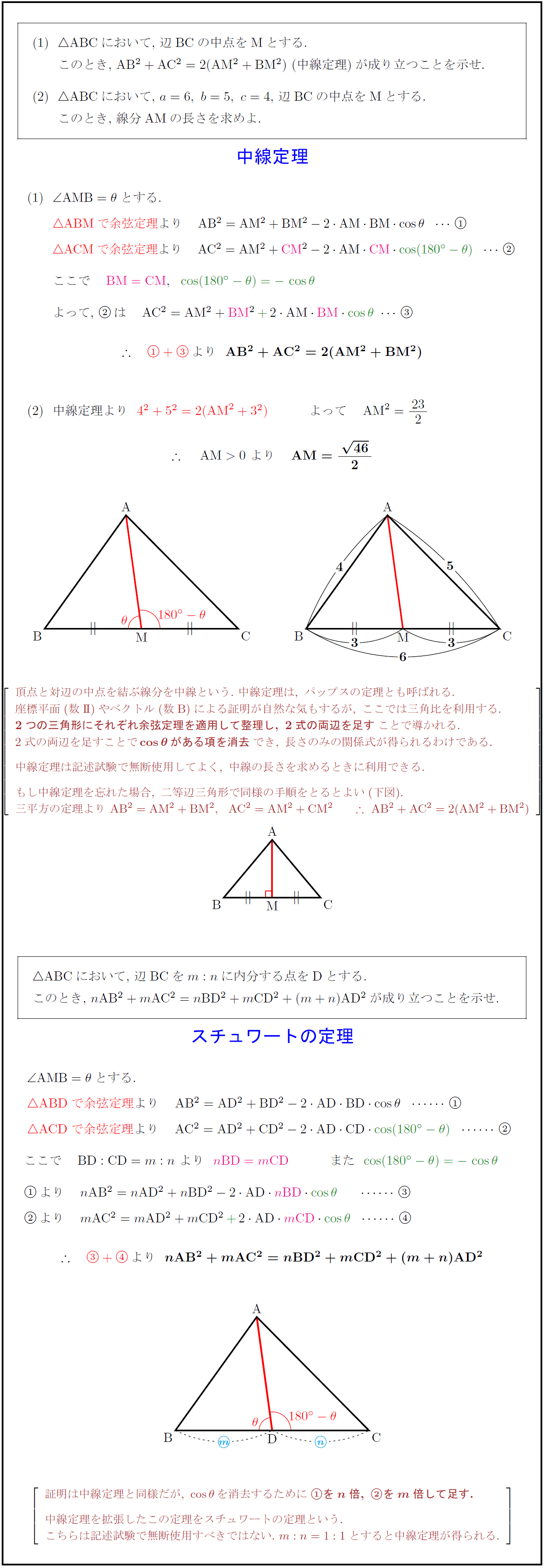


高校数学 中線定理 パップスの定理 とスチュワートの定理の三角比による証明 受験の月



Sankakuhi



高校 数学 三角比31 平行四辺形の面積 6分 Youtube



円に内接する四角形 小学5年への説明 再掲 Okwave



高校数学b ベクトルの成分表示と平行四辺形 受験の月



直交対角線四角形 Wikipedia


Www Chart Co Jp Subject Sugaku Suken Tsushin 79 79 6 Pdf



平行四辺形を中学生でもわかるように解説 性質 証明を即理解 高校生向け受験応援メディア 受験のミカタ


平行四辺形とは 定義 条件 性質や面積の公式 証明問題 受験辞典



これは平行四辺形を二つに分けて三角形として考えれば良いのでしょうか 解説お願いします Clear



平行四辺形を中学生でもわかるように解説 性質 証明を即理解 高校生向け受験応援メディア 受験のミカタ


平行四辺形とは 定義 条件 性質や面積の公式 証明問題 受験辞典
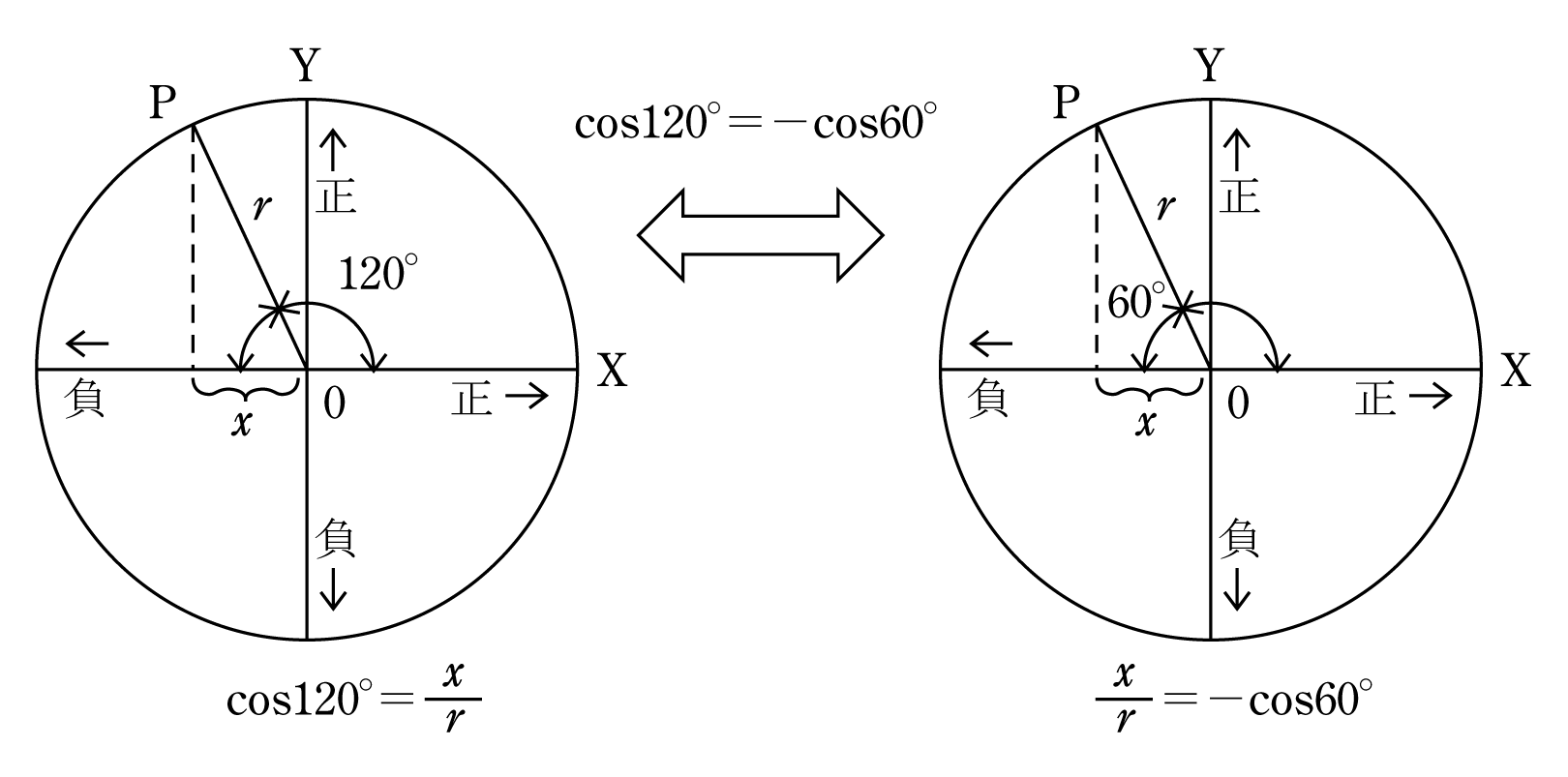


余弦定理と交流ベクトル計算への応用 音声付き電気技術解説講座 公益社団法人 日本電気技術者協会



平行四辺形を中学生でもわかるように解説 性質 証明を即理解 高校生向け受験応援メディア 受験のミカタ



三角形の面積


平行四辺形とは 定義 条件 性質や面積の公式 証明問題 受験辞典



0 件のコメント:
コメントを投稿